|
Size: 2489
Comment:
|
← Revision 53 as of 2021-06-21 18:07:44 ⇥
Size: 7486
Comment:
|
| Deletions are marked like this. | Additions are marked like this. |
| Line 7: | Line 7: |
| = resp = | = RESP: module for response properties based on HF and DFT = |
| Line 10: | Line 11: |
| {{{ Response properties based on DFT/HF theory. }}} |
== Quick guides by examples == The following examples give the minimal inputs for starting response calculations (Input files and benchmark results can be found in '''bdf-pkg/tests/input/resp2014'''): 1. [[Ground-state geometric derivatives]] 1. [[Excited-state properties based on analytic derivatives]] 1. [[Response properties based on response functions|Response properties based on linear and quadratic response functions]] 1. [[Examples: first-order nonadiabatic couplings|First-order nonadiabatic couplings]] 1. [[Alternative of TD-DFT: particle-particle TDA (pp-TDA) based properties]] |
| Line 14: | Line 20: |
| == Keywords == |
== Keywords for general information == |
| Line 17: | Line 22: |
| Line 22: | Line 26: |
| === METHOD === | === CTHRD === |
| Line 24: | Line 28: |
| === IGNORE === -1: recomputes the TD-DFT excitation energy. This is mainly intended as an internal consistency check, to see if the implementation of $resp and $tddft are mutually consistent. For NAC calculations, this additionally prints the Hellmann-Feynman NAC (which is identical to the exact NAC in the infinite basis set limit but converges very slowly as the basis set is enlarged) for informational purposes. <<BR>> 0: default<<BR>> 1: skip the skewness check of Wmo. The skewness of the Wmo matrix is theoretically zero, but can obtain finite values when the TD-DFT and/or the Z-vector iterations are not fully converged, or if the program has a bug. The program by default aborts if the skewness of Wmo exceeds <<latex($3\times 10^{-5}$)>>, and analyzes the possible reason for this deviation (either TD-DFT or Z-vector did not fully converge, or both). Setting ignore=1 bypasses this check so that the calculation can continue, but the results may be inaccurate. == Keyworks for processing excited-state information == === IMETHOD,METHOD === |
|
| Line 26: | Line 37: |
| CHCK GEOM LINE QUAD FNAC POLA HYPE FDIF AOPER BOPER COPER BFREQ CFREQ REDUCED NORESP IGNORE SINGLE STATES DOUBLE PAIRS STEP BOHR NORDER CTHRD IPROPS NFILES |
=== NFILES === Linked with '''istore''' value in TD-DFT input for loading output. |
| Line 53: | Line 40: |
| == Quick guides by examples == The following examples give the minimal inputs for starting response calculations: |
== Keyword for geometric derivatives == === GEOM: NORDER === GEOM enables geometric derivatives, NORDER=1, gradient and fo-NACMEs; =2, hessian (not implemented yet.) |
| Line 56: | Line 44: |
| === Example: first-order NAC === | === IREP and IROOT === Specify which root should be followed in a TD-DFT gradient calculation. Example: {{{ irep 2 iroot 3 }}} requests the calculation of the TD-DFT gradient of the 3rd excited state of the 2nd irrep, while {{{ iroot 3 }}} will calculate the TD-DFT gradient of the 3rd lowest excited state among all irreps. That is, the excited states of all irreps are sorted in ascending order according to excitation energy, and the 3rd excited state is followed. |
| Line 58: | Line 59: |
| === JAHNTELLER === When the excited state is degenerate due to symmetry reasons, the molecule will undergo Jahn-Teller distortion (unless the molecule is linear), but there is some arbitrariness in the direction of the distortion. For example, a molecule with <<latex($I_h$)>> symmetry in the triplet degenerate <<latex($T_{2g}$)>> excited state can reduce its symmetry into any one of the following groups: <<latex($D_{2h}$)>>, <<latex($D_{3d}$)>>, <<latex($D_{5d}$)>>, as well as their subgroups. Therefore, in a TD-DFT geometry optimization, the point group symmetry of the molecule in the second geometry optimization step may be lower than the molecule in the first geometry optimization step. With the JAHNTELLER keyword, one can specify the point group symmetry of the distorted molecule and thereby guide the geometry optimization in the correct direction. For example: |
|
| Line 59: | Line 62: |
| jahnteller D(2h) }}} requests that the Jahn-Teller distorted molecule should have at least <<latex($D_{2h}$)>> symmetry. If this is impossible due to group theoretic reasons, the program prints a warning and ignores the user input. The default behavior is to keep the highest symmetry possible: thus, in the aforementioned case, the geometry optimization will continue with <<latex($D_{5d}$)>> symmetry, since this preserves the five-fold axis. |
|
| Line 60: | Line 67: |
| $COMPASS Title nh3 Basis sto-3g Geometry C 0.00000000 -1.20809142 -1.14173975 C 0.00000000 -1.20797607 0.25342015 C 0.00000000 0.00000000 0.95085852 C -0.00000000 1.20797607 0.25342015 C -0.00000000 1.20809142 -1.14173975 C 0.00000000 0.00000000 -1.83922155 H 0.00000000 -2.16045397 -1.69142002 H 0.00000000 -2.16044427 0.80300713 H -0.00000000 2.16044427 0.80300713 H -0.00000000 2.16045397 -1.69142002 H 0.00000000 0.00000000 -2.93882555 F 0.00000000 0.00000000 2.30085848 End geometry skeleton group c(1) nosym $END |
== Keywords for linear response calculations == === LINE === Enable linear response |
| Line 85: | Line 71: |
| $xuanyuan direct schwarz $end |
=== REDUCED === Solve the response equation in its reduced form [(A-B)(A+B)-w2](X+Y)=Rvo+Rov (not preferred). |
| Line 90: | Line 74: |
| $scf RHF charge 0 spin 1 THRESHCONV 1.d-10 1.d-8 OPTSCR 1 iaufbau 0 $end |
=== POLA: AOPER, BOPER, BFREQ === Polarizabiity: '''<<A;B>>(wB)''', where the operators A and B can be dipole (DIP), quadruple (QUA), SOC (HSO), EFG. |
| Line 104: | Line 77: |
| $tddft imethod 1 isf 0 iexit 2 itda 1 idiag 1 istore 1 crit_e 1.d-10 crit_vec 1.d-8 lefteig AOKXC DirectGrid $end |
== Keywords for quadratic response calculations == === QUAD === Enable quadratic response function (QRF) calculations |
| Line 126: | Line 81: |
| $resp iprt 1 QUAD FNAC single states 1 1 1 2 double pairs 1 1 1 1 1 1 2 norder 1 method 2 nfiles 1 FDIF step 0.001 ignore 1 noresp $end |
=== HYPE: AOPER, BOPER, BFREQ, COPER, CFREQ === Hyperpolarizability: '''<<A;B,C>>(wB,wC)''' |
| Line 153: | Line 84: |
| }}} | === SINGLE:STATES === Single residue of QRF, STATES can be used to specify the number of states followed by a detailed specification via the triple (ifile,isym,istate). |
| Line 155: | Line 87: |
| To use finite-difference, a script '''fdiff.py''' should be used as {{{ ./fbdiff.py run.sh input.inp > log }}} After the calculation is done, an output file '''input.out''' will present in the current directory. The '''log''' file saves the information during the calculations. |
=== DOUBLE: PAIRS === Double residue of QRF, PAIRS can be used to specify the number of pairs followed by a detailed specification via two triples (ifile,isym,istate,jfile,isym,jstate). |
| Line 161: | Line 90: |
| Note: If '''FDIF''' is omitted, the analytic calculation will be carried out by simply using the '''run.sh''' script. | === FNAC === First-order nonadiabatic couplings === NORESP === Neglect the response part of transition density matrix in DOUBLE and FNAC calculations (recommended) == Keywords for finite difference calculations == === FDIF === Enable finite difference calculations === STEP === followed by a real number for the step size, default 0.001 [unit]. === BOHR === The default unit is angstrom, to use bohr. This keyword must be specified. = Some caveats before using this module = As for now, the resp module supports all pure functionals and simple hybrid functionals, but not including the LibXC functionals (B97 etc.). For '''range-separated hybrids''', only properties that do not involve nuclear derivatives (e.g. dipole moments, polarizabilities, hyperpolarizabilities, SOC corrections, etc.) are supported (again, this does not include the LibXC range-separated hybrids, e.g. wB97, wB97X etc., which are not supported at all); we are working on extending the scope of applicability to properties that do involve nuclear derivatives (gradients, NACMEs). '''Double hybrids''' are not yet supported, and will not be supported in the near future. === scf === The following requirements are for finite-difference NAC only. 1. Tight convergence on density matrix is required (10^-14^). 2. '''sgnfix''': fix adjacent sign of MOs during SCF iterations 3. '''iaufbau'''=3: fix ordering and sign with respect to the initial MOs. For gradients and analytic NACs, the default SCF convergence criteria are likely sufficient. For numerical Hessians the default convergence criteria give frequencies that are accurate to a couple of cm^-1. In cases where spurious imaginary frequencies arise, it may be necessary to tighten the convergence criteria further. === tddft === 1. Tight convergence on eigenvectors (10^-6^) and eigenvalues (10^-8^). The default criteria (10^-5^ and 10^-7^, respectively) are frequently insufficient. 2. When self-adaptive XC integration grid is used, it is recommended to tighten '''gridtol''' in $tddft, especially for open-shell systems. Recommended value is 10^-7^. 3. Keyword '''lefteig''' should be used for storing left eigenvectors in TD-DFT 4. Keyword '''istore''' speficify the file number of TD-DFT calculations |
RESP: module for response properties based on HF and DFT
Contents
- RESP: module for response properties based on HF and DFT
- Some caveats before using this module
Quick guides by examples
The following examples give the minimal inputs for starting response calculations (Input files and benchmark results can be found in bdf-pkg/tests/input/resp2014):
Response properties based on linear and quadratic response functions
Alternative of TD-DFT: particle-particle TDA (pp-TDA) based properties
Keywords for general information
IPRT
Print level, >1 gives more information, >2 give more information about integral evaluations.
NPRT
CTHRD
IGNORE
-1: recomputes the TD-DFT excitation energy. This is mainly intended as an internal consistency check, to see if the implementation of $resp and $tddft are mutually consistent. For NAC calculations, this additionally prints the Hellmann-Feynman NAC (which is identical to the exact NAC in the infinite basis set limit but converges very slowly as the basis set is enlarged) for informational purposes.
0: default
1: skip the skewness check of Wmo. The skewness of the Wmo matrix is theoretically zero, but can obtain finite values when the TD-DFT and/or the Z-vector iterations are not fully converged, or if the program has a bug. The program by default aborts if the skewness of Wmo exceeds 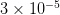 , and analyzes the possible reason for this deviation (either TD-DFT or Z-vector did not fully converge, or both). Setting ignore=1 bypasses this check so that the calculation can continue, but the results may be inaccurate.
, and analyzes the possible reason for this deviation (either TD-DFT or Z-vector did not fully converge, or both). Setting ignore=1 bypasses this check so that the calculation can continue, but the results may be inaccurate.
Keyworks for processing excited-state information
IMETHOD,METHOD
=1, ground state gradients; =2, excited-state calculations which will load TD-DFT output.
NFILES
Linked with istore value in TD-DFT input for loading output.
Keyword for geometric derivatives
GEOM: NORDER
GEOM enables geometric derivatives, NORDER=1, gradient and fo-NACMEs; =2, hessian (not implemented yet.)
IREP and IROOT
Specify which root should be followed in a TD-DFT gradient calculation. Example:
irep 2 iroot 3
requests the calculation of the TD-DFT gradient of the 3rd excited state of the 2nd irrep, while
iroot 3
will calculate the TD-DFT gradient of the 3rd lowest excited state among all irreps. That is, the excited states of all irreps are sorted in ascending order according to excitation energy, and the 3rd excited state is followed.
JAHNTELLER
When the excited state is degenerate due to symmetry reasons, the molecule will undergo Jahn-Teller distortion (unless the molecule is linear), but there is some arbitrariness in the direction of the distortion. For example, a molecule with 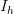 symmetry in the triplet degenerate
symmetry in the triplet degenerate 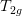 excited state can reduce its symmetry into any one of the following groups:
excited state can reduce its symmetry into any one of the following groups: 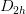 ,
, 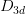 ,
, 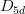 , as well as their subgroups. Therefore, in a TD-DFT geometry optimization, the point group symmetry of the molecule in the second geometry optimization step may be lower than the molecule in the first geometry optimization step. With the JAHNTELLER keyword, one can specify the point group symmetry of the distorted molecule and thereby guide the geometry optimization in the correct direction. For example:
, as well as their subgroups. Therefore, in a TD-DFT geometry optimization, the point group symmetry of the molecule in the second geometry optimization step may be lower than the molecule in the first geometry optimization step. With the JAHNTELLER keyword, one can specify the point group symmetry of the distorted molecule and thereby guide the geometry optimization in the correct direction. For example:
jahnteller D(2h)
requests that the Jahn-Teller distorted molecule should have at least 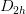 symmetry. If this is impossible due to group theoretic reasons, the program prints a warning and ignores the user input. The default behavior is to keep the highest symmetry possible: thus, in the aforementioned case, the geometry optimization will continue with
symmetry. If this is impossible due to group theoretic reasons, the program prints a warning and ignores the user input. The default behavior is to keep the highest symmetry possible: thus, in the aforementioned case, the geometry optimization will continue with 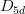 symmetry, since this preserves the five-fold axis.
symmetry, since this preserves the five-fold axis.
Keywords for linear response calculations
LINE
Enable linear response
REDUCED
Solve the response equation in its reduced form [(A-B)(A+B)-w2](X+Y)=Rvo+Rov (not preferred).
POLA: AOPER, BOPER, BFREQ
Polarizabiity: <<A;B>>(wB), where the operators A and B can be dipole (DIP), quadruple (QUA), SOC (HSO), EFG.
Keywords for quadratic response calculations
QUAD
Enable quadratic response function (QRF) calculations
HYPE: AOPER, BOPER, BFREQ, COPER, CFREQ
Hyperpolarizability: <<A;B,C>>(wB,wC)
SINGLE:STATES
Single residue of QRF, STATES can be used to specify the number of states followed by a detailed specification via the triple (ifile,isym,istate).
DOUBLE: PAIRS
Double residue of QRF, PAIRS can be used to specify the number of pairs followed by a detailed specification via two triples (ifile,isym,istate,jfile,isym,jstate).
FNAC
First-order nonadiabatic couplings
NORESP
Neglect the response part of transition density matrix in DOUBLE and FNAC calculations (recommended)
Keywords for finite difference calculations
FDIF
Enable finite difference calculations
STEP
followed by a real number for the step size, default 0.001 [unit].
BOHR
The default unit is angstrom, to use bohr. This keyword must be specified.
Some caveats before using this module
As for now, the resp module supports all pure functionals and simple hybrid functionals, but not including the LibXC functionals (B97 etc.). For range-separated hybrids, only properties that do not involve nuclear derivatives (e.g. dipole moments, polarizabilities, hyperpolarizabilities, SOC corrections, etc.) are supported (again, this does not include the LibXC range-separated hybrids, e.g. wB97, wB97X etc., which are not supported at all); we are working on extending the scope of applicability to properties that do involve nuclear derivatives (gradients, NACMEs). Double hybrids are not yet supported, and will not be supported in the near future.
scf
The following requirements are for finite-difference NAC only.
1. Tight convergence on density matrix is required (10-14).
2. sgnfix: fix adjacent sign of MOs during SCF iterations
3. iaufbau=3: fix ordering and sign with respect to the initial MOs.
For gradients and analytic NACs, the default SCF convergence criteria are likely sufficient. For numerical Hessians the default convergence criteria give frequencies that are accurate to a couple of cm^-1. In cases where spurious imaginary frequencies arise, it may be necessary to tighten the convergence criteria further.
tddft
1. Tight convergence on eigenvectors (10-6) and eigenvalues (10-8). The default criteria (10-5 and 10-7, respectively) are frequently insufficient.
2. When self-adaptive XC integration grid is used, it is recommended to tighten gridtol in $tddft, especially for open-shell systems. Recommended value is 10-7.
3. Keyword lefteig should be used for storing left eigenvectors in TD-DFT
4. Keyword istore speficify the file number of TD-DFT calculations