Differences between revisions 32 and 53 (spanning 21 versions)

RESP: module for response properties based on HF and DFT

Contents

RESP: module for response properties based on HF and DFT
Some caveats before using this module
1. 1. scf
  2. tddft

Quick guides by examples

The following examples give the minimal inputs for starting response calculations (Input files and benchmark results can be found in bdf-pkg/tests/input/resp2014):

Keywords for general information

IPRT

Print level, >1 gives more information, >2 give more information about integral evaluations.

NPRT

CTHRD

IGNORE

-1: recomputes the TD-DFT excitation energy. This is mainly intended as an internal consistency check, to see if the implementation of $resp and $tddft are mutually consistent. For NAC calculations, this additionally prints the Hellmann-Feynman NAC (which is identical to the exact NAC in the infinite basis set limit but converges very slowly as the basis set is enlarged) for informational purposes.
0: default
1: skip the skewness check of Wmo. The skewness of the Wmo matrix is theoretically zero, but can obtain finite values when the TD-DFT and/or the Z-vector iterations are not fully converged, or if the program has a bug. The program by default aborts if the skewness of Wmo exceeds 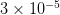$3\times 10^{-5}$ , and analyzes the possible reason for this deviation (either TD-DFT or Z-vector did not fully converge, or both). Setting ignore=1 bypasses this check so that the calculation can continue, but the results may be inaccurate.

Keyworks for processing excited-state information

IMETHOD,METHOD

=1, ground state gradients; =2, excited-state calculations which will load TD-DFT output.

NFILES

Linked with istore value in TD-DFT input for loading output.

Keyword for geometric derivatives

GEOM: NORDER

GEOM enables geometric derivatives, NORDER=1, gradient and fo-NACMEs; =2, hessian (not implemented yet.)

IREP and IROOT

Specify which root should be followed in a TD-DFT gradient calculation. Example:

irep
2
iroot
3

requests the calculation of the TD-DFT gradient of the 3rd excited state of the 2nd irrep, while

iroot
3

will calculate the TD-DFT gradient of the 3rd lowest excited state among all irreps. That is, the excited states of all irreps are sorted in ascending order according to excitation energy, and the 3rd excited state is followed.

JAHNTELLER

When the excited state is degenerate due to symmetry reasons, the molecule will undergo Jahn-Teller distortion (unless the molecule is linear), but there is some arbitrariness in the direction of the distortion. For example, a molecule with 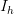$I_h$ symmetry in the triplet degenerate 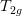$T_{2g}$ excited state can reduce its symmetry into any one of the following groups: 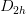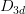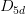$D_{2h}$ , $D_{3d}$ , $D_{5d}$ , as well as their subgroups. Therefore, in a TD-DFT geometry optimization, the point group symmetry of the molecule in the second geometry optimization step may be lower than the molecule in the first geometry optimization step. With the JAHNTELLER keyword, one can specify the point group symmetry of the distorted molecule and thereby guide the geometry optimization in the correct direction. For example:

jahnteller
D(2h)

requests that the Jahn-Teller distorted molecule should have at least 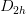$D_{2h}$ symmetry. If this is impossible due to group theoretic reasons, the program prints a warning and ignores the user input. The default behavior is to keep the highest symmetry possible: thus, in the aforementioned case, the geometry optimization will continue with 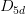$D_{5d}$ symmetry, since this preserves the five-fold axis.

Keywords for linear response calculations

LINE

Enable linear response

REDUCED

Solve the response equation in its reduced form [(A-B)(A+B)-w2](X+Y)=Rvo+Rov (not preferred).

POLA: AOPER, BOPER, BFREQ

Polarizabiity: <<A;B>>(wB), where the operators A and B can be dipole (DIP), quadruple (QUA), SOC (HSO), EFG.

Keywords for quadratic response calculations

QUAD

Enable quadratic response function (QRF) calculations

HYPE: AOPER, BOPER, BFREQ, COPER, CFREQ

Hyperpolarizability: <<A;B,C>>(wB,wC)

SINGLE:STATES

Single residue of QRF, STATES can be used to specify the number of states followed by a detailed specification via the triple (ifile,isym,istate).

DOUBLE: PAIRS

Double residue of QRF, PAIRS can be used to specify the number of pairs followed by a detailed specification via two triples (ifile,isym,istate,jfile,isym,jstate).

FNAC

First-order nonadiabatic couplings

NORESP

Neglect the response part of transition density matrix in DOUBLE and FNAC calculations (recommended)

Keywords for finite difference calculations

FDIF

Enable finite difference calculations

STEP

followed by a real number for the step size, default 0.001 [unit].

BOHR

The default unit is angstrom, to use bohr. This keyword must be specified.

Some caveats before using this module

As for now, the resp module supports all pure functionals and simple hybrid functionals, but not including the LibXC functionals (B97 etc.). For range-separated hybrids, only properties that do not involve nuclear derivatives (e.g. dipole moments, polarizabilities, hyperpolarizabilities, SOC corrections, etc.) are supported (again, this does not include the LibXC range-separated hybrids, e.g. wB97, wB97X etc., which are not supported at all); we are working on extending the scope of applicability to properties that do involve nuclear derivatives (gradients, NACMEs). Double hybrids are not yet supported, and will not be supported in the near future.

scf

The following requirements are for finite-difference NAC only.

1. Tight convergence on density matrix is required (10^-14).

2. sgnfix: fix adjacent sign of MOs during SCF iterations

3. iaufbau=3: fix ordering and sign with respect to the initial MOs.

For gradients and analytic NACs, the default SCF convergence criteria are likely sufficient. For numerical Hessians the default convergence criteria give frequencies that are accurate to a couple of cm^-1. In cases where spurious imaginary frequencies arise, it may be necessary to tighten the convergence criteria further.

tddft

1. Tight convergence on eigenvectors (10^-6) and eigenvalues (10^-8). The default criteria (10^-5 and 10^-7, respectively) are frequently insufficient.

2. When self-adaptive XC integration grid is used, it is recommended to tighten gridtol in $tddft, especially for open-shell systems. Recommended value is 10^-7.

3. Keyword lefteig should be used for storing left eigenvectors in TD-DFT

4. Keyword istore speficify the file number of TD-DFT calculations

-  ⇤ ← Revision 32 as of 2014-09-27 02:55:02 → 
  Size: 3603
  Editor: 162
  Comment:
+   ← Revision 53 as of 2021-06-21 18:07:44 → ⇥
  Size: 7486
  Editor: wangzikuan
  Comment:
-Deletions are marked like this.
+Additions are marked like this.
 Line 7:
-= RESP module for response properties based on HF and DFT =
+= RESP: module for response properties based on HF and DFT =
 Line 11:
-== Keywords ==
+== Quick guides by examples ==
The following examples give the minimal inputs for starting response calculations
(Input files and benchmark results can be found in '''bdf-pkg/tests/input/resp2014'''): 
 1. [[Ground-state geometric derivatives]]
 1. [[Excited-state properties based on analytic derivatives]]
 1. [[Response properties based on response functions|Response properties based on linear and quadratic response functions]]
 1. [[Examples: first-order nonadiabatic couplings|First-order nonadiabatic couplings]]
 1. [[Alternative of TD-DFT: particle-particle TDA (pp-TDA) based properties]]
-Line 18:
+Line 25:
-=== CHCK ===
Check the interface with several external packages.
-Line 22:
+Line 27:
+=== IGNORE ===
-1: recomputes the TD-DFT excitation energy. This is mainly intended as an internal consistency check, to see if the implementation of $resp and $tddft are mutually consistent. For NAC calculations, this additionally prints the Hellmann-Feynman NAC (which is identical to the exact NAC in the infinite basis set limit but converges very slowly as the basis set is enlarged) for informational purposes. <<BR>>
0: default<<BR>>
1: skip the skewness check of Wmo. The skewness of the Wmo matrix is theoretically zero, but can obtain finite values when the TD-DFT and/or the Z-vector iterations are not fully converged, or if the program has a bug. The program by default aborts if the skewness of Wmo exceeds <<latex($3\times 10^{-5}$)>>, and analyzes the possible reason for this deviation (either TD-DFT or Z-vector did not fully converge, or both). Setting ignore=1 bypasses this check so that the calculation can continue, but the results may be inaccurate.
-Line 23:
+Line 34:
-=== METHOD ===
+=== IMETHOD,METHOD ===
-Line 32:
+Line 43:
+=== IREP and IROOT ===
Specify which root should be followed in a TD-DFT gradient calculation. Example:
{{{
irep
2
iroot
3
}}}
requests the calculation of the TD-DFT gradient of the 3rd excited state of the 2nd irrep, while
{{{
iroot
3
}}}
will calculate the TD-DFT gradient of the 3rd lowest excited state among all irreps. That is, the excited states of all irreps are sorted in ascending order according to excitation energy, and the 3rd excited state is followed.

=== JAHNTELLER ===
When the excited state is degenerate due to symmetry reasons, the molecule will undergo Jahn-Teller distortion (unless the molecule is linear), but there is some arbitrariness in the direction of the distortion. For example, a molecule with <<latex($I_h$)>> symmetry in the triplet degenerate <<latex($T_{2g}$)>> excited state can reduce its symmetry into any one of the following groups: <<latex($D_{2h}$)>>, <<latex($D_{3d}$)>>, <<latex($D_{5d}$)>>, as well as their subgroups. Therefore, in a TD-DFT geometry optimization, the point group symmetry of the molecule in the second geometry optimization step may be lower than the molecule in the first geometry optimization step. With the JAHNTELLER keyword, one can specify the point group symmetry of the distorted molecule and thereby guide the geometry optimization in the correct direction. For example:
{{{
jahnteller
D(2h)
}}}
requests that the Jahn-Teller distorted molecule should have at least <<latex($D_{2h}$)>> symmetry. If this is impossible due to group theoretic reasons, the program prints a warning and ignores the user input. The default behavior is to keep the highest symmetry possible: thus, in the aforementioned case, the geometry optimization will continue with <<latex($D_{5d}$)>> symmetry, since this preserves the five-fold axis.
-Line 72:
+Line 106:
-=== IGNORE ===
Ignore the recomputation of excitation energies for check consistency.

= Quick guides by examples =
The following examples give the minimal inputs for starting response calculations:

 1. [[Ground-state geometric derivatives]]
 1. [[Response properties based on response functions|Response properties based on linear and quadratic response functions]]
 1. [[Excited-state properties based on analytic derivatives]]
 1. [[Examples: first-order nonadiabatic couplings|First-order nonadiabatic couplings]]
 1. [[Alternative of TD-DFT: particle-particle TDA (pp-TDA) based properties]]
-Line 86:
+Line 108:
-=== dft ===

1. Thresholds in dft_prescreen.F90 have been set very tight.

2. Keyword '''ixcfun''' in SCF allows to use original XC library (default) or XCFun lib (=1) by Ulf Ekström [http://www.admol.org/xcfun] in dft and tddft.
+As for now, the resp module supports all pure functionals and simple hybrid functionals, but not including the LibXC functionals (B97  etc.). For '''range-separated hybrids''', only properties that do not involve nuclear derivatives (e.g. dipole moments, polarizabilities, hyperpolarizabilities, SOC corrections, etc.) are supported (again, this does not include the LibXC range-separated hybrids, e.g. wB97, wB97X etc., which are not supported at all); we are working on extending the scope of applicability to properties that do involve nuclear derivatives (gradients, NACMEs). '''Double hybrids''' are not yet supported, and will not be supported in the near future.
-Line 94:
+Line 112:
-. Tight convergence on density matrix is required.
+The following requirements are for finite-difference NAC only.

1. Tight convergence on density matrix is required (10^-14^).
-Line 98:
+Line 118:
-. '''iaufbau'''=3: fix ordering and sign with respect to the initial MOs.
+. '''iaufbau'''=3: fix ordering and sign with respect to the initial MOs.

For gradients and analytic NACs, the default SCF convergence criteria are likely sufficient. For numerical Hessians the default convergence criteria give frequencies that are accurate to a couple of cm^-1. In cases where spurious imaginary frequencies arise, it may be necessary to tighten the convergence criteria further.
-Line 103:
+Line 125:
-. Tight convergence on eigenvectors
+. Tight convergence on eigenvectors (10^-6^) and eigenvalues (10^-8^). The default criteria (10^-5^ and 10^-7^, respectively) are frequently insufficient.
-Line 105:
+Line 127:
-. Keyword '''lefteig''' for storing left eigenvectors in TD-DFT
+. When self-adaptive XC integration grid is used, it is recommended to tighten '''gridtol''' in $tddft, especially for open-shell systems. Recommended value is 10^-7^.
-Line 107:
+Line 129:
-. '''istore''' key the file number of TD-DFT calculations
+. Keyword '''lefteig''' should be used for storing left eigenvectors in TD-DFT

4. Keyword '''istore''' speficify the file number of TD-DFT calculations

Quick Links

Search Wiki

Page Tools